Ray-tracing(2) Barycentric Interpolation

Sep 10, 2022

Barycentric coordinate

Barycentric coordinate interpolation is used to interpolate any point or any attribute of a vertex for in an interior triangle. In this raytracing project, I implement barycentric interpolation to calculate the value of the normal vector at the position of the ray intersection point and return it as an RGBs value.

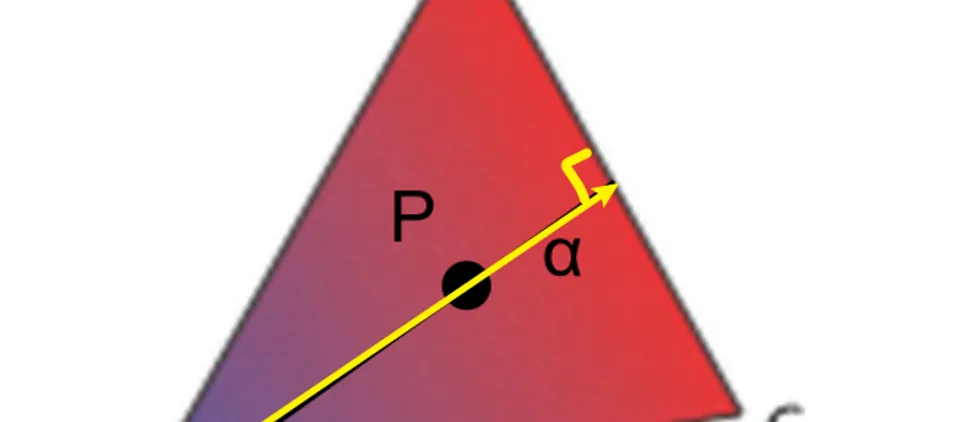
Assume the triangle ΔABC, suppose we assign 100% blue color at vertex A and 0% blue at CB. The intensity varies linearly perpendicular to BC. The amount of color at any point within the triangle is determined by its distance from the edges.We can represent the color intensity or any other value at point $P$ within the triangle using the barycentric coordinates $\alpha$ , $\beta$ , $\gamma$ :

\alpha = \frac{dist(P,\vec{BC})}{dist(A,\vec{BC})}

Do the same thing to other 2 parameters:

\beta = \frac{dist(P,\vec{CA})}{dist(B,\vec{CA})}

\gamma = \frac{dist(P,\vec{AB})}{dist(C,\vec{AB})}

Notice that $\alpha + \beta + \gamma = 1$ . Hence, we only need to compute 2 of the parameters. So, any point in the triangle could have a representation of barycentric coordinate. And we could do interpolation directly in this.

for (int x = xMin; x < xMax; x++){
	for (int y = yMin; y < yMax; y++) {
	    float alpha = distance((x, y), BC) / distance(A, BC);
	    float beta = distance((x, y), AC) / distance(B, AC);
	    float gamma = 1 - alpha - beta;
	    
	    if (alpha < 0.0 || beta < 0.0 || gamma < 0.0)
	        continue;
	
	    Color color = alpha * color(A) + beta * color(B) + gamma * color(C);
	    setPixel(x, y, color);
	}
}

Implementation

Triangle.cpp | Leeds-Raytracing | Github

Cartesian3 Triangle::Baricentric(Cartesian3 o) {  
  
    // Input is the intersection between the ray and the triangle.  
  
    // two edges of a triangle (NOTICE: CCW)    
    Cartesian3 E1 = (verts[2] - verts[1]).Vector();  
    Cartesian3 E2 = (verts[0] - verts[2]).Vector();  
  
    // compute distances to edges  
    Cartesian3 distance1 = o - verts[1].Vector();  
    Cartesian3 distance2 = o - verts[2].Vector();  
  
    // two normals  
    Cartesian3 na = E1.cross(distance1);  
    Cartesian3 nb = E2.cross(distance2);  
  
    // compute normal of the triangle by edges  
    Cartesian3 N = E1.cross(E2);  
  
    // we can use na.length() / N.length() directly,   
    // but sqrt() is more costly   
    // while the normal is same plane as the na and nb, so using dot() and square() is more effective.  
    // meanwhile, N.square() could also represent the area of the triangle.   
	// Thus, Area method and Length Method are same  
    float normLenSquare = N.square();  
    float alpha = N.dot(na) / normLenSquare;  
    float beta = N.dot(nb) / normLenSquare;  
  
    return Cartesian3{alpha, beta, 1 - alpha - beta};  
}

something should be noticed the square of the normal has two times area as the triangle. To analze it, assume two vectors $u$ , $v$ were given. the length of cross producet would be:

\Vert u \Vert \times v \Vert= \Vert u \Vert \cdot \Vert v\Vert \cot \sin(\theta)

where, $θ$ is the angle between $u$ and $v$ . Thus, this equation gives the area of the parallelogram.

Ray-tracing(2) Barycentric Interpolation

Barycentric coordinate

Implementation

Reference