STL Containers - Set

set vs. vector

• They are both containers that can store a series of data.
• Difference 1: The set automatically sorts its elements in ascending order, while the vector maintains the order in which elements were inserted.
• Difference 2: The set removes duplicate elements, keeping only one instance of each, effectively removing duplicates.
• Difference 3: Elements in a vector are stored in contiguous memory, allowing for efficient random access by index, whereas this is not the case for a set.
• Difference 4: Elements in a set can be efficiently searched by value, while a vector has less efficient value-based searching.

vector<int> a {9, 8, 5, 2, 1, 1};
cout << "vector => " << a << endl;
set<int> b {9, 8, 5, 2, 1, 1};
cout << "set    => " << b << endl;

Sorting of set

• The set sorts in ascending order, which is based on numerical comparison for integers.
• For strings, sorting is done in “lexicographical order” The string class defines the < operator overload, which compares two strings lexicographically based on ASCII values.
• If they are equal, it continues comparing the next characters, and if they are not equal, it returns the result of that comparison. If it reaches the end of both strings and they are equal in length, they are considered equal.

vector<string> a = {"arch", "any", "zero", "Linux"};
cout << "vector=" << a << endl;
set<string> b = {"arch", "any", "zero", "Linux"};
cout << "set=" << b << endl;

Warning: Never use set<char *> for string collections. This will only compare the addresses of string pointers, not the content they point to.

Custom Sorting Functions

• The set class, as a template class, actually has two template parameters: set<T, CompT> .
• The first parameter, T , specifies the type of elements in the container, such as int or string .
• The second parameter, CompT , defines the comparison functor you want to use. The set internally invokes this function to determine how to perform the sorting.
• If CompT is not specified, the default behavior is to use the < operator for comparison.
• Here, we define a myComp functor for comparison, and it’s the same as the default behavior using < , so there is no change in sorting.

auto myComp = [](string const &a, string const &b){
	return a < b;
};
set<string, myComp> b = {"arch", "any", "zero", "Linux"};
cout << "set=" << b << endl;

Using the following approach, we can implement a case-insensitive comparison for the set:

auto myComp = [](string const &a, string const &b){
	std::transform(a.begin(), a.end(), a.begin(), ::tolower);
	std::transform(b.begin(), b.end(), b.begin(), ::tolower);
	return a < b;
};
set<string, myComp> b = {"arch", "any", "zero", "Linux"};
cout << "set=" << b << endl;
return 0;

Traversal

for (auto it = b.begin(); it != b.end(); ++it) {
	int value = *it;
	cout << value << endl;
}

• C++11 introduced a syntactic sugar: the range-based for loop.

for (auto&& value : b) {
    cout << value << endl;
}

• Using two iterators for traversal, you can also utilize the iterators returned by lower_bound and upper_bound to select elements satisfying the condition 2 ≤ x ≤ 4 and print them.

for (auto it = b.lower_bound(2); it != b.upper_bound(4); ++it) {
    int value = *it;
    cout << value << endl;
}

Size of a set

Commonalities of set and vector Iterators

• vector provides two member functions, begin() and end() , which return iterators pointing to the first element and one past the last element in the array, respectively.
• both have a size() function to determine the number of elements it contains.

set<int> b = {1, 2, 3, 4, 5};
cout << "Original set: " << b << endl;
cout << "Number of elements: " << b.size() << endl;

• In the case of vector , since it is a contiguous array, its iterators are essentially equivalent to pointers.
• set also has begin() and end() functions, but the iterators they return are overloaded with the * operator to access the address they point to.

vector<int> a = {1, 2, 3, 4, 5, 6, 7};
vector<int>::iterator a_it = a.begin();
cout << "vector[0]=" << *a_it << endl;

set<int> b = {1, 2, 3, 4, 5, 6, 7};
set<int>::iterator b_it = b.begin();
cout << "set[0]=" << *b_it << endl;
// set<int>::iterator b_it = b.begin() + 3; // Error! No such operator

• vector provides overloaded + and += operators for iterators, while set does not. This is because elements in a vector are stored in contiguous memory, allowing for random access.
• After C++11, set uses a red-black tree for implementation internally, and the iterator objects are essentially for traversing the red-black tree. Therefore, a set is not contiguous and supports only sequential access, not random access.
• So, attempting to use b.begin() + 3 as shown in the code will result in an error.
• set provides overloaded ++ for traversal of the red-black tree.

set<int> b = {1, 2, 3, 4, 5, 6, 7};
set<int>::iterator b_it = b.begin();
++b_it;
++b_it;
++b_it;

std::next is equivalent to +

• Manually writing three ++ operations as shown above can be cumbersome and modifies the iterator itself. STL provides the std::next function, which internally behaves like this:

auto next(auto it, int n = 1)
{
	if (it is random_access)
		return it + n;

	while (n--)
		++it;
	return it;
}

• It automatically checks whether the iterator supports the + operation. If not, it resorts to a less efficient method of calling ++ n times.

vector<int> a = {1, 2, 3, 4, 5, 6, 7};
vector<int>::iterator a_it = a.begin();
a_it = std::next(a_it, 3);  // Calls a_it + 3
cout << "vector[3]=" << *a_it << endl;

set<int> b = {1, 2, 3, 4, 5, 6, 7};
set<int>::iterator b_it = b.begin();
b_it = std::next(b_it, 3);  // Calls ++b_it three times
cout << "set[3]=" << *b_it << endl;

std::advance is equivalent to +=

• The std::next function, as mentioned earlier, returns the incremented iterator. In contrast, std::advance increments the iterator in place when passed by reference and has no return value. It also checks whether += is supported to determine which implementation to use.

void advance(auto& it, int n)
{
	if (it is random_acess) {
		it += n;
	} else {
		while (n--)
			++it;
	}
}

• The key difference is that advance modifies the iterator in place, without returning a new iterator, whereas next modifies the iterator and returns the modified iterator.

next and advance support negative numbers

• While the iterator type is bidirectional, next also accepts negative values for n , which means it moves the iterator backward. For example, std::next(it, -3) is equivalent to it - 3 . Another dedicated function, std::prev(it, 3) , which is also equivalent to it - 3 .

auto next(auto it, int n = 1) {
	if (it is random_access)
		return it + n;
	else{
		if (it is bidirectional && n < 0) {
			while (n++)
				--it;
		}
		while (n--)
			++it;
		return it;
	}
}

void advance(auto& it, int n)
{
	if (it is random_acess) {
		it += n;
	} else{
		if (it is bidirectional && n < 0) {
			while (n++)
				--it;
		}
		while (n--)
			++it;
	}
}

std::distance is equivalent to right - left .

• std::distance calculates the distance (difference) between two iterators.
• std::distance(it1, it2) is equivalent to it2 - it1 , with the order reversed.
• Note: distance requires it1 < it2 .

vector<int> a = {1, 2, 3, 4, 5, 6, 7};
vector<int>::iterator a_it1 = a.begin();
vector<int>::iterator a_it2 = a.end();
// Calls a_it2 - a_it1

int a_size = std::distance(a_it1, a_it2);
cout << "vector size = " << a_size << endl;
set<int> b = {1, 2, 3, 4, 5, 6, 7};
set<int>::iterator b_it1 = b.begin();
set<int>::iterator b_it2 = b.end();
// Calls ++b_it1 until it equals b_it2
int b_size = std::distance(b_it1, b_it2);
cout << "set size = " << b_size << endl;

Insertion

• You can add an element to a set by calling the insert function. You don’t need to worry about the insertion position; for example, when inserting the element 3, the set will automatically place it between 2 and 4, ensuring that the elements are always arranged in ascending order.

set<int> b = {1, 4, 2, 1};
cout << "Before insertion: " << b << endl;
b.insert(3);
cout << "After insertion: " << b << endl;

cout << "Before insertion: " << b << endl;
b.insert(4);
cout << "After insertion: " << b << endl;

Return values of insert

• The insert function returns a pair type, which means it returns two values simultaneously. The second return value is of type bool and indicates whether the insertion was successful.

pair<iterator, bool> insert(int val);

• If an element with the same value already exists in the set container, the insertion fails, and the bool value is false. If the element does not exist in the set, the insertion succeeds, and the bool value is true.

set<int> b = {1, 4, 2, 1};
auto [ok1, it1] = b.insert(3);
cout << "Insertion of 3 successful: " << ok1 << endl;
cout << "Position of 3: " << *it1 << endl;

auto [ok2, it2] = b.insert(3);
cout << "Insertion of 3 again successful: " << ok2 << endl;
cout << "Position of 3: " << *it2 << endl;

The first return value is an iterator, and it depends on two scenarios:

1. When adding an element to the set container is successful, the iterator points to the newly added element in the set container, and the bool value is true.
2. If the insertion fails, meaning that the set container already contains an element with the same value, the returned iterator points to the existing element in the container, and the bool value is false.

Search

Find element in a Set

Sets have a find function. You only need to provide one parameter, and it will search for an element in the set that is equal to the given value.

• If found, it returns an iterator pointing to the found element.
• If not found, it returns the end() iterator.

set<int> b = {1, 4, 2, 1};
auto it = b.find(2);
cout << "Position of 2: " << *it << endl;
cout << "Number smaller than 2: " << *prev(it) << endl;
cout << "Number greater than 2: " << *next(it) << endl;

• As mentioned earlier, end() points to one past the last element of the set, representing an address that does not exist. It is commonly used as a marker to indicate that the element was not found, similar to how Python’s find returns -1 when an element is not found.

set<int> b = {1, 4, 2, 1};
if (b.find(2) != b.end()) cout << "2 is in the set" << endl;
else cout << "2 is not in the set" << endl;

count() and contains()

• There is another, more straightforward way to check for the existence of an element:
• set.count(x) != 0
• count returns an int type, indicating the number of equal elements in the set. which is the STL considered the generality of the interface because, after all, multiset doesn’t remove duplicates. For sets that do remove duplicates, count can only return 0 or 1.
• A count of 0 means the element is not in the set. A count of 1 means the element exists in the set. Because an int type can be implicitly converted to a bool , you can omit != 0 .
• After C++20, it provides contains which is same as count for set .

set<int> b = {1, 4, 2, 1};
if (b.count(2)) {
    cout << "2 is in the set" << endl;
} else {
    cout << "2 is not in the set" << endl;
}

if (b.contains(8)) {
    cout << "8 is in the set" << endl;
} else {
    cout << "8 is not in the set" << endl;
}

Deletion

Removing a element by calling erase()

set.erase(x) can be used to delete elements in the set with a value of x . erase returns an integer representing the number of elements removed by it.

• If returns 0, it means that the element was not in the set, and the deletion failed.
• If returns 1, it means that the element was in the set, and the deletion was successful.

set<int> b = {1, 2, 3, 4, 5};
cout << "Before deletion: " << b << endl;
int num = b.erase(4);
cout << "After deletion: " << b << endl;
cout << "Deleted " << num << " element(s)" << endl;

Removing a element by iterator

erase also supports iterators as parameters.

• set.erase(it) can delete the element at the position specified by the iterator it . Examples of usage:
• set.erase(set.find(x)) will delete the element with a value of x from the set, which is equivalent to set.erase(x) .
• set.erase(set.begin()) will delete the smallest element in the set because sets automatically sort their elements, and the element at the front is always the smallest.
• set.erase(std::prev(set.end())) will delete the largest element in the set because of the automatic sorting feature, and the element at the end is always the largest.

set<int> b = {1, 2, 3, 4, 5};
cout << "Original set: " << b << endl;
b.erase(b.find(4));
cout << "After deleting 4: " << b << endl;
b.erase(b.begin());
cout << "After deleting the smallest element: " << b << endl;
b.erase(std::prev(b.end()));
cout << "After deleting the largest element: " << b << endl;

Removing Elements in a Specified Range from a Set

erase also supports taking two iterators as parameters.

• set.erase(beg, end) can delete elements in the set from beg to end , including beg but excluding end . In other words, it is a half-open range [beg, end) , following the usual convention in the standard library. - Note: beg must be before end , or it will result in a crash.
• Example of usage: a.erase(a.find(2), a.find(4)) will delete all elements in the set satisfying 2 ≤ x < 4 (because sets are automatically sorted, so deleting elements between the iterators 2 and 4 is equivalent to deleting elements satisfying 2 ≤ x < 4 ).

set<int> b = {1, 2, 3, 4, 5};
cout << "Original set: " << b << endl;
b.erase(b.find(2), b.find(4));
cout << "After deleting elements in the range [2, 4): " << b << endl;

But this method has a significant problem: What if there is no 2 in the set? In that case, find(2) will return end() , and find(4) will successfully find the iterator pointing to 4 . This means that the iterator from find(2) (which is actually end() ) comes after the iterator from find(4) , violating the rule that “beg must be before end,” which can lead to a crash.

The right method is to use lower_bound and upper_bound Functions

lower_bound and upper_bound Functions

The function lower_bound(x) searches for the first element greater than or equal to x . And upper_bound(x) searches for the first element greater than x . When they can’t find an element, they all return end() .

• lower_bound(2) will return an iterator pointing to 3 .
• upper_bound(2) will also return an iterator pointing to 3 .
• find(2) will simply say “not found” and return end() .

auto check(bool success) {
	if (!success) throw;
	cout << "Test passed" << endl;
};
set<int> b = {0, 1, 3, 4, 5};

cout << "Original set: " << b << endl;
check(b.find(2) == b.end());
check(b.lower_bound(2) == b.find(3));
check(b.upper_bound(2) == b.find(3));

So, we could these two functions to implement safe and right range deletion for a set:

set<int> b = {1, 2, 3, 4, 5};
cout << "Original set: " << b << endl;
b.erase(b.lower_bound(2), b.upper_bound(4));
cout << "After deleting elements in the range [2, 4): " << b << endl;

Clear set Elements

There are three ways to clear a set. The most common one is to call the clear function, which has the same name as the clear function in a vector.

set<int> b = {1, 2, 3, 4, 5};
cout << "Original set: " << b << endl;
b.clear();
// b = {};
// b.erase(b.begin(), b.end());
cout << "Set after clearing: " << b << endl;

Summary of set Operations

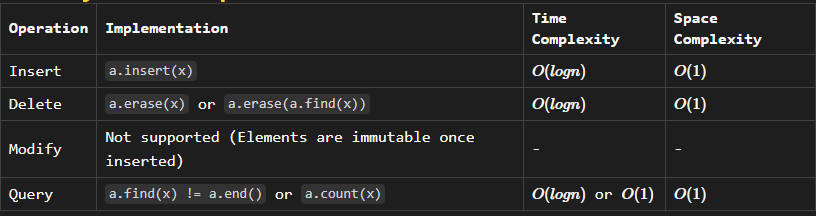
Note:

• Time complexity is based on the assumption that the set is implemented as a balanced binary search tree (e.g., Red-Black Tree).
• Space complexity refers to the additional space required for set data structure itself, excluding the space for elements stored in the set.

Convserions with Other Containers

set and vector

The constructor of a vector can also accept two forward iterators as parameters, and set iterators meet this requirement. So, we can copy a range of elements from the set (2 ≤ x ≤ 4) into a vector. This is essentially a way to filter out all elements where 2 ≤ x ≤ 4.

set<int> b = {0, 1, 3, 4, 5};
cout << "Original set: " << b << endl;
vector<int> arr(b.lower_bound(2), b.upper_bound(4));
cout << "Resulting array: " << arr << endl;

Directly using vector(b.begin(), b.end()) to copy all the elements from the set into the vector, which is the most common use case.

set<int> b = {0, 1, 3, 4, 5};
cout << "Original set: " << b << endl;
vector<int> arr(b.begin(), b.end());
cout << "Resulting array: " << arr << endl;

It can also reverse the process and convert a vector to a set.

• To convert to a vector container: vector(b.begin(), b.end())
• To convert to a set container: set(b.begin(), b.end())

vector<int> b = {0, 1, 3, 4, 5};
cout << "Original array: " << b << endl;
set<int> arr(b.begin(), b.end());
cout << "Resulting set: " << arr << endl;

Clever Use of Sets: Sorting and De-duplication

Here’s a method to sort and remove duplicates from a vector using a set:

vector<int> arr = {9, 8, 5, 2, 1, 1};
cout << "Original array: " << arr << endl;

set<int> b(arr.begin(), arr.end());
arr.assign(b.begin(), b.end());

cout << "Sorted & de-duplicated array: " << arr << endl;

This code converts the vector arr into a set b , which automatically sorts its elements and removes duplicates. Then, it assigns the elements from the set b back to the vector arr , resulting in a sorted and de-duplicated array.

A Non-Distinct Sibling: Multiset

A set has the characteristics of automatic sorting, automatic deduplication, and efficient querying, resembling mathematical sets. However, there’s another version, multiset , that doesn’t remove duplicates but still maintains automatic sorting and efficient querying. Characteristics of Multisets:

• Multisets allow duplicate elements while preserving automatic sorting.
• All equal elements in a multiset are placed together, resulting in structures like {1, 2, 2, 4, 6} .

set<int> a = {1, 1, 2, 2, 3};
multiset<int> b = {1, 1, 2, 2, 3};

cout << "set: " << a << endl;
cout << "multiset: " << b << endl;

Finding Equal-Value Ranges in a Multiset

equal elements are placed together in a multisets, using upper_bound and lower_bound functions to obtain the range of all equal values: [lower_bound, upper_bound) .

cout << "Original multiset: " << b << endl;
b.erase(b.lower_bound(2), b.upper_bound(2));
cout << "After removing 2: " << b << endl;

For cases where the arguments to lower_bound and upper_bound are the same, you can use equal_range to efficiently retrieve both boundaries of the equal-value range.

multiset<int> b = {1, 1, 2, 2, 3};

cout << "Original multiset: " << b << endl;
auto r = b.equal_range(2);
b.erase(r.first, r.second);
cout << "After removing 2: " << b << endl;

The difference between equal_range and calling lower_bound (greater than or equal to the starting point) and upper_bound (greater than the starting point) twice is:

• When the specified value is not found, equal_range returns two end() iterators, indicating an empty range.
• lower/upper_bound , on the other hand, will return iterators pointing to elements greater than or equal to the specified value. The reason for this difference is that equal_range is intended for efficiently obtaining a range for traversal where both iterators are used together and are never used separately. So, when no equal elements are found, it returns an empty range directly for efficiency.

Erasing Elements in a Multiset

The version of erase with a single parameter will delete all elements equal to 2 in the multiset.

multiset<int> b = {1, 1, 2, 2, 3};

cout << "Original multiset: " << b << endl;
b.erase(2);
cout << "After removing 2: " << b << endl;

For example: b.erase(2) is equivalent to b.erase(b.lower_bound(2), b.upper_bound(2)) .

Counting Equal Elements by count()

The count(x) function returns the number of elements equal to x in the multiset (returns 0 if not found).

multiset<int> b = {1, 1, 2, 2, 3};

cout << "Original multiset: " << b << endl;
auto r = b.equal_range(6);

cout << boolalpha;
cout << (r.first == b.end()) << endl;
cout << (r.second == b.end()) << endl;

r = b.equal_range(2);
size_t n = std::distance(r.first, r.second);
cout << "Number of elements equal to 2: " << n << endl;

for (auto it = r.first; it != r.second; ++it) {
    int value = *it;
    cout << value << endl;
}

In contrast to sets (which have deduplication), the count function in multisets can return any non-negative number.

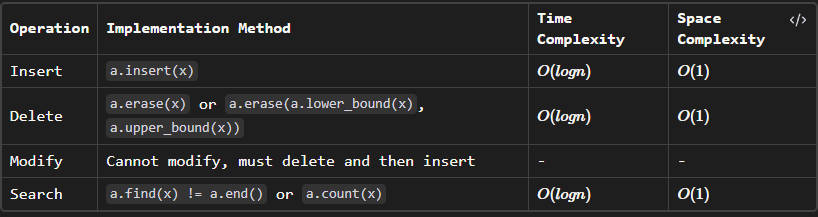
Please note that the time complexity mentioned here is for typical cases in a balanced multiset. In the worst-case scenario, some of these operations may take $O(n)$ time, but that’s rare.

C++11 New Member: unordered_set Container

• set arranges elements in ascending order.
• unordered_set does not sort elements; the order is entirely random and differs from the order of insertion.
• set is implemented based on a red-black tree, similar to a binary search tree. In contrast, unordered_set is based on a hash table, and the random order is a result of the hash function.

vector<int> arr(100);
auto comp = [&] (int i, int j) {
	return arr[i] < arr[j];
};

set<int, decltype(comp)> a({1, 4, 2, 8, 5, 7}, comp);
unordered_set<int> b = {1, 4, 2, 8, 5, 7};

cout << "set: " << a << endl;
cout << "unordered_set: " << b << endl;

unordered_set<tuple<int, int>> Hash Error

Using unordered_set<tuple<int, int>> will result in an error because by default, tuple doesn’t have a hash function defined, and unordered_set requires a hash function to determine the storage location of elements. Here’s an example:

// Custom hash function using XOR operation on the hash values of tuple elements
struct TupleHash {
    template <class T1, class T2>
    std::size_t operator() (const std::tuple<T1, T2>& t) const {
        auto h1 = std::hash<T1>{}(std::get<0>(t));
        auto h2 = std::hash<T2>{}(std::get<1>(t));
        return h1 ^ h2;
    }
};

int main() {
	auto tupleHash = [](const auto& t) {
	    auto h1 = std::hash<typename std::tuple_element<0, decltype(t)>::type>{}(std::get<0>(t));
	    auto h2 = std::hash<typename std::tuple_element<1, decltype(t)>::type>{}(std::get<1>(t));
	    return h1 ^ h2;
	};

    std::unordered_set<std::tuple<int, int>, TupleHash> myuSet;

    myuSet.emplace(1, 2);
    myuSet.emplace(2, 3);
    myuSet.emplace(1, 2); // This element is a duplicate but won't cause an error

    for (const auto& t : myuSet) {
        std::cout << std::get<0>(t) << ", " << std::get<1>(t) << std::endl;
    }

    return 0;
}

In this example, we defined a hash function object named TupleHash to calculate the hash value of tuples. When creating the unordered_set , we explicitly specify the type of this hash function object.

Summary of unordered_set Operations

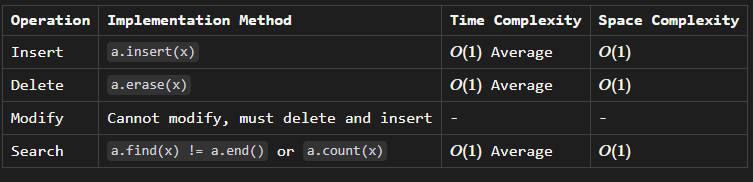
Please note that the time complexity for insert and delete operations in an unordered_set is typically O(1) on average due to the use of hashing. However, in the worst-case scenario, these operations can become O(n), where n is the number of elements in the container.

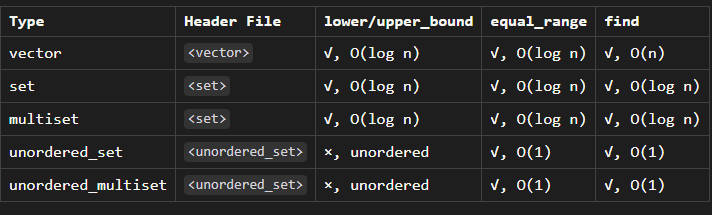
Summary of Set Family Member Operations

Please note that unordered_set does not support lower_bound and upper_bound functions because it does not maintain order. Additionally, for set and multiset , the count(x) function returns either 0 or 1 since these containers do not allow duplicate elements.

Summary of Set Family

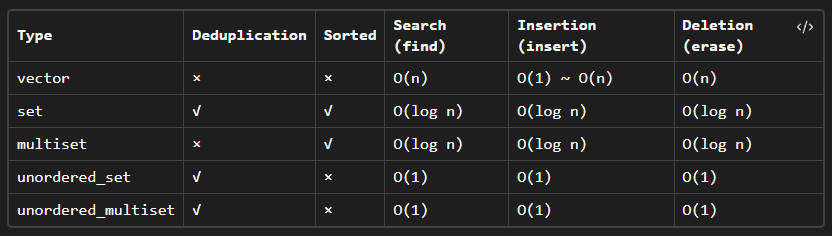
Regarding the suitable use cases for different containers in terms of lookup:

• vector Suitable for index-based lookups, accessed using the [] operator.
• set : Suitable for value-based equal, greater-than, and less-than lookups, using functions like find, lower_bound, and upper_bound.
• unordered_set : Suitable only for value-based equal lookups, using the find function.

As a general recommendation, if you’re working with smaller datasets, set might be more efficient for lookups. However, for larger datasets (typically >1000 elements), unordered_set could offer better average lookup times, but it doesn’t guarantee stability.